بررسی منحنی هیسترزیس به همراه مثال های نمودار هیسترزیس اعضای سازه ­ای

همانطور که می دانید منحنی هیسترزیس جهت بررسی رفتار مصالح، تحت بار رفت و برگشتی در زمان وقوع زلزله مورد استفاده قرار می‌گیرد. برای انجام تحلیل های غیر خطی سازه، شناخت رفتار عضو و منحنی هیسترزیس آن ضروری است اما پدیده هیسترزیس چیست؟ با توجه به منحنی هیسترزیس در چه مقاطعی می توانیم جذب انرژی بهتری داشته باشیم؟ ویژگی نمودار هیسترزیس چیست؟ سطح زیر منحنی هیسترزیس چگونه اندازه گیری می شود؟

در این مقاله به بررسی صفر تا صد منحنی هیسترزیس می پردازیم و به تمامی سوالات شما پاسخ خواهیم داد. برای درک درست مطالب حتما ویدئو ابتدای صفحه را یک بار مشاهده کنید.

⌛ آخرین به‌روزرسانی: 22 تیرماه 1401

📕 تغییرات به‌روزرسانی: تکمیل مطالب قبلی و اضافه شدن مطالب جدید

1. منحنی تنش-کرنش و تعریف نقاط مختلف این نمودار

پیش از ورود به بحث منحنی‌های هیسترزیس (Hysteresis Curves)، با توجه به اینکه این منحنی به نوعی تکمیل‌شده‌ی منحنی تنش-کرنش (و یا نیرو-جابه‌جایی) می‌باشد، لازم است ابتدا اندکی در رابطه با منحنی تنش-کرنش توضیح داده شود. در واقع منحنی هیسترسیس همان منحنی تنش-کرنش می‌باشد با این تفاوت که به جای بارگذاری یکنواخت (Monotonic)، بارگذاری به صورت سیکلی (رفت و برگشتی) انجام شده و المان به طور متناوب تحت کشش و فشار قرار می‌گیرد.

منحنی تنش-کرنش برای یک المان شکل‌پذیر، در شکل زیر مشاهده می‌شود. این منحنی تحت بارگذاریِ یکنواختِ کششی بدست آمده است. در صورتی­که این منحنی برای کل به­ دست آید به آن منحنی ظرفیت سازه گویند.

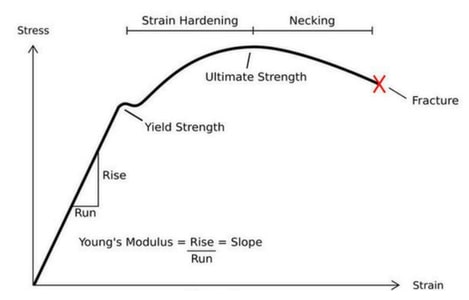
شکل 1: نمودار تنش-کرنش مصالح شکل‌پذیر

این منحنی از نقاط مختلفی تشکیل شده که برای مصالح شکل‌پذیر، شامل 6 نقطه‌ی اصلی می‌باشد که در شکل زیر مشخص شده‌اند، در ادامه به توضیح هر یک از آن‌ها پرداخته شده است:

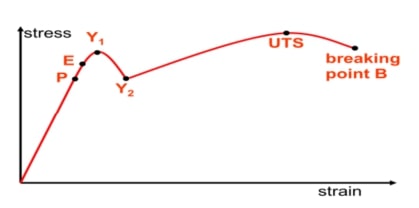
شکل 2: نقاط مختلف در نمودار تنش-کرنش مصالح

• حد خطی یا σ_PL) Proportional Limit): این حد نقطه‌ی P در شکل فوق می‌باشد. این نقطه نشان‌دهنده‌ی حدی است که تا رسیدن به آن تنش و کرنش رابطه‌ی خطی با یکدیگر دارند. شیب این خط مدول الاستیسیته یا E نامیده می‌شود. پس از عبور از این نقطه رابطه‌ی تنش و کرنش دیگر خطی نخواهد بود. برای یک عضو بتن مسلح که قبل از نقطه شروع تسلیم ترک می­خورد، رفتار اولیه می‌تواند اساسا غیرخطی باشد. هرچند زمانی که عضو بتنی ترک خورده باشد، هنگام باربرداری و بارگذاری مجدد، رفتار اولیه آن تقریبا خطی خواهد بود. به عنوان یک مثال دیگر، برخی از اجزا اتصالاتی که امکان لغزش پیچ در آن­ها وجود دارد، ممکن است پیش از تسلیم شدن، رفتار اتصال غیرخطی داشته باشد.
• حد الاستیک یا σ_EL) Elastic Limit): مرحله‌ی بعدی در نمودار نقطه‌ی E می‌باشد که به آن حد الاستیک گفته می‌شود. این نقطه در واقع نشان‌دهنده‌ی حداکثر تنشی‌ است که می‌توان به المان وارد نمود بدون آنکه دچار تغییرشکل‌های دائمی‌شود. در واقع تا قبل از رسیدن به این حد، اگر باربرداری انجام شود کرنش‌های به وجود آمده کاملاً از بین رفته و نمونه به حالت اولیه بازمی‌گردد. در حد الاستیک، تنش و کرنش رابطه‌ی خطی ندارند. برای فولادهای ساختمانی حد خطی و حد الاستیک بسیار به یکدیگر نزدیک می‌باشند.
• تنش تسلیم یا σ_Y) Yield Stress): نقطه‌ی ، نشان‌دهنده‌ی حد تسلیم یا(جاری شدن) المان می‌باشد. با رسیدن به این حد با افزایش بسیار اندکِ تنش، کرنش به‌شدت افزایش می‌یابد و نمونه دچار تغییرشکل‌های دائمی می‌شود. در این حالت بدون افزایش بار، ماده شروع به تغییرشکل می‌نماید. در فولاد ساختمانی، این نقطه هم بسیار نزدیک به نقاط حد خطی و الاستیک است. برای فولاد، دو نوع حد تسلیم تعریف ‌می‌شود:

1. 1. حد تسلیم بالایی (Upper Yield Point)
   2. حد تسلیم پایینی (Lower Yield Point)

این دو حد تسلیم در شکل فوق باY₁ وY₂ نشان داده شده‌اند.

• تنش نهایی یا (σ_U) Ultimate Tensile Strength (UTS) : نقطه بعدی در نمودار فوق، با نماد UTS نشان داده شده، مربوط به تنش نهایی است. معمولا این حد مقاومت بعد از تغییرشکل­های غیرارتجاعی و سخت­شدگی کرنشی حاصل می­شود. این حد در واقع حداکثر تنشی است که نمونه تحمل می‌نماید، پس از آن نمودار شیب نزولی خواهد داشت.
• تنش گسیختگی یا σ_F) Fracture Stress): آخرین مرحله‌ای هم که ماده به آن می‌رسد، تنش گسیختگی نام دارد. نقطه‌ی B در شکل فوق نشان‌دهنده‌ی این تنش است. با رسیدن به این تنش، نمونه دچار شکست (گسیختگی) می‌شود.

2. بررسی ویژگی‌های ناحیه‌ی الاستیک و غیر الاستیک و مفهوم شکل پذیری

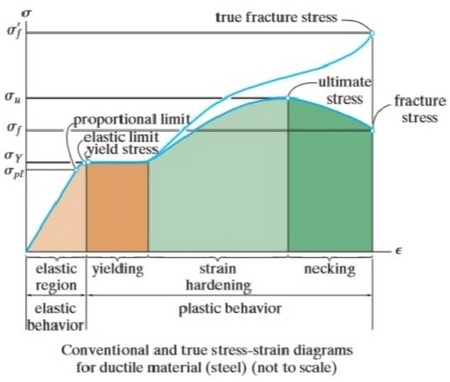
شکل 3: ناحیه‌های تشکیل شده در منحنی تنش-کرنش

علاوه بر نقاط مختلفی که در این نمودار وجود دارد و معرفی گردید، منحنی تنش-کرنش به نواحی مختلفی تقسیم می‌شود. در شکل فوق، ناحیه‌ها به دو بخش اصلی الاستیک و پلاستیک (غیر الاستیک) تقسیم شد‌ه‌اند.

• ناحیه‌ی الاستیک: این ناحیه تا تنش σ_EL (Elastic Limit) ادامه داشته و تا قبل از رسیدن به آن، تغییرشکل‌های المان برگشت‌پذیر خواهند بود. در واقع در ناحیه‌ی الاستیک با برداشتن بار، شکل و سایز المان به حالت اولیه باز خواهند گشت.
• ناحیه‌ی پلاستیک: با رسیدن به تنش الاستیک (σ_EL) (Elastic Limit) ناحیه‌ی پلاستیک شروع و تا تنش گسیختگی σ_f ادامه می‌یابد. تغییرشکل‌های این ناحیه قابل‌برگشت نخواهند بود. ناحیه‌ی پلاستیک به سه بخش اصلی تقسیم می‌شود:

1. 1. ناحیه‌ی تسلیم (Yielding): در این ناحیه بدون افزایش قابل‌ملاحظه‌ی بار، کرنش به سرعت زیاد می‌شود.
   2. ناحیه‌ی سخت‌شوندگی کرنشی (Strain Hardening): ناحیه‌ای که بین تنش تسلیم بالایی و تنش نهایی قرار دارد، ناحیه‌ی سخت‌شوندگی کرنشی نامیده می‌شود. در این ناحیه، با زیاد شدن تنش المان افزایش طول داده تا به حد ماکسیمم تنش یعنی تنش نهایی (σ_u) برسد. در این ناحیه سطح مقطع عضو به صورت یکنواخت کاهش می‌یابد.
   3. ناحیه‌ی باریک شدگی (Necking): ناحیه‌ی پایانی هم که بین تنش نهایی و تنش گسیختگی قرار دارد، ناحیه‌ی باریک شدگی یا Necking نام دارد. در این ناحیه سطح مقطع عضو در یک نقطه به صورت متمرکز کاهش‌یافته و توانایی مقطع در تحمل بار هم کم می‌شود. در شکل زیر، حالت مقطع در این مرحله مشاهده می‌شود:

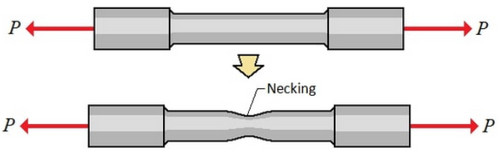
شکل 4:  پدیده‌ی باریک شدگی (Necking) در مقطع

همان‌طور که گفته شد، درصورتی‌که با رسیدن به ناحیه‌ی پلاستیک باربرداری صورت گیرد، تنها بخشی از کرنش برگشت‌پذیر بوده و بخشی از تغییرشکل به وجود آمده، ماندگار می‌باشد و از بین نخواهد رفت. در شکل زیر این تغییرشکل‌ها مشاهده می‌شوند. لازم به ذکر است که شیب منحنی باربرداری با شیب منحنی اولیه برابر و مساوی با E است.

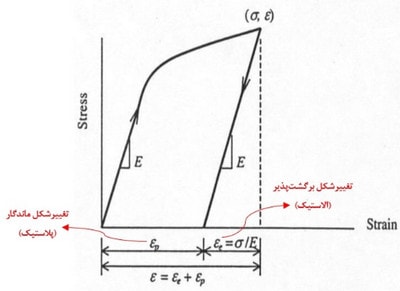
شکل 5: بارگذاری و باربرداری در ناحیه‌ی پلاستیک

با توجه به شکل فوق، مشخص است که بعد از ورود به ناحیه‌ی تغییرشکل‌های پلاستیک، کرنش المان برابر با ε است که این کرنش به دو بخش کرنش الاستیک (ε_e) و کرنش پلاستیک (ε_p) تقسیم می‌شود.

 نکته:

همان‌طور که در شکل مربوط به ناحیه‌های مختلف در منحنی تنش-کرنش مشاهده شد، منحنی تنش کرنش از یک نقطه به بعد به دوشاخه تبدیل شده است. یکی از این شاخه منحنی تنش-کرنش واقعی (True) و دیگری منحنی تنش-کرنش مهندسی (Engineering) نامیده می‌شود.

درصورتی‌که بخواهیم منحنی دقیق یا واقعی را محاسبه نماییم در تمام طول آزمایش باید سطح مقطع المان اندازه‌گیری شده و برای محاسبه‌ی تنش از آن استفاده شود. اما در حالت مهندسی از این تغییر مساحت المان صرف‌نظر کرده و از سطح مقطع اولیه برای محاسبه‌ی تنش در هر لحظه، استفاده می‌شود.

نکته:

  یکی از خصوصیات مصالح که پس از بدست آمدن نمودار تنش-کرنش می‌توان محاسبه نمود، شکل‌پذیری نامیده می‌شود. شکل‌ پذیری به صورت نسبت کرنش متناظر با حد نهایی، به کرنش متناظر با حد تسلیم تعریف می‌شود. در شکل زیر تعریف این پارامتر مشاهده می‌شود. شکل‌ پذیری نشان‌ دهنده‌ی قابلیت جذب انرژی مواد است.

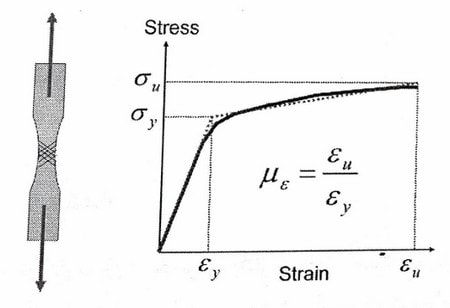
شکل 6: تعریف شکل‌پذیری مصالح

رفتار فولاد به عنوان یک آلیاژ، بسیار تابع درصد کربن موجود در ترکیبات شیمیایی اولیه می‌باشد. به‌ طوری‌ که با افزایش کربن، مقاومت فولاد افزایش یافته اما به موجب آن شکل‌ پذیری کاهش می‌یابد. در شکل زیر نمودار تنش-کرنش فولاد با درصد کربن‌ های مختلف مشاهده می‌ شود.

فولاد ساختمانی که حدود 0.2% کربن دارد هم در این نمودار مشخص شده است. در حالت کلی فولاد مورد استفاده در ساختمان، فولاد کم کربن نامیده می‌شود زیرا رفتار مطلوب برای اعضای سازه‌ ای، رفتاری شکل‌ پذیر می‌باشد.

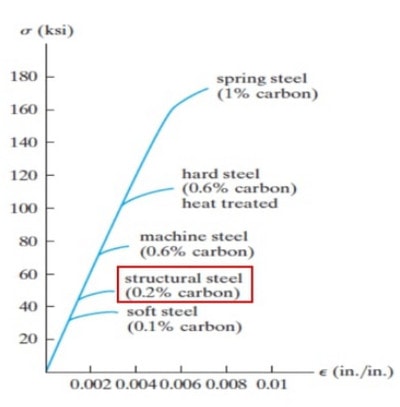
شکل 7: درصد کربن موجود در فولادهای مختلف و تاثیر آن در افزایش مقاومت

منحنی ظرفیت سازه یا منحنی تنش_کرنش عضو با استفاده از تحلیل استاتیکی غیرخطی (پوش اور) قابل محاسبه هستند. از طرفی به خاطر ماهیت رفت و برگشتی زلزله، اطلاعات کامل و دقیق­تری از رفتار عضو یا سازه به ما ارائه نمی­دهند و نیاز به تحلیل تاریخچه زمانی غیرخطی است.

مشکلی که در انجام تحلیل­ های غیرخطی وجود دارد این است که تهیه مدل سازه­ای برای انجام تحلیل غیرارتجاعی طوری که نتایج قابل­قبول و منطبق با نتایج آزمایشگاهی به ­دست آید، نه تنها احتیاج به تعیین سختی المان­ها (مثل تحلیل­های خطی) دارد بلکه به سایر مشخصات اعضا نظیر مقاومت، سخت­ شدگی کرنشی، حد شکل­ پذیری و شکل حلقه­ های هیسترزیس وابسته است. با این اوصاف شاید به اهمیت حلقه ­های هیسترزیس در مد­ل‌سازی رفتار واقعی و غیرخطی سازه پی‌برده باشید تا بتوان سازه­ای ایمن در مقابل زلزله­ های شدید طرح و اجرا کرد.

رفتار غیرخطی می­تواند دارای پیچیدگی­ ها و عدم قطعیت­ های بسیاری باشد. تهیه مدل­ های غیرخطی مناسب برای تحلیل سازه، مستلزم فهم دقیق از رفتار غیرخطی اعضای سازه ­ای است. در بخش­ های بعد با منحنی­ های هیسترزیس و ویژگی­ های مربوط به آن بیشتر آشنا می­شویم.

3. تعریف منحنی هیسترزیس، تفاوت ویژگی مصالح در بارگذاری یکنواخت و بارگذاری متناوب

در بخش قبل رفتار غیرخطی یک المان، تحت بارگذاری یکنواخت (Monotonic)، بررسی گردید. به منحنی تنش-کرنش که ممکن است به صورت نیرو-تغییرمکان یا ممان-انحنا هم بررسی شود، Backbone Curve گفته می‌شود. این منحنی علاوه بر اینکه برای هر المان سازه ای بدست می آید، برای کل سازه هم قابل محاسبه است.

اما علاوه بر این منحنی، رفتار غیرخطی را تحت بارهای سیکلی هم می‌توان بررسی نمود که در این حالت به آن منحنی هیسترزیس (Hysteresis Curve ) گفته می‌شود. یک نمونه از این منحنی در شکل زیر مشاهده می‌شود که متشکل از چندین حلقه، ناشی از سیکل‌های مختلف بارگذاری می‌باشد.

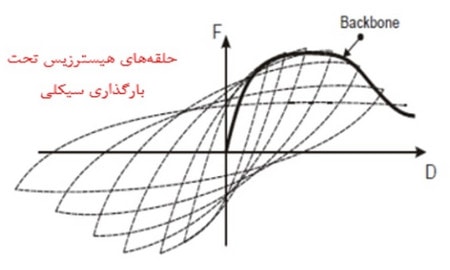
شکل 8:  یک نمونه منحنی هیسترزیس به همراه Backbone Curve حاصل از این منحنی

نمونه‌ای از Backbone Curve که برای منحنی‌ های هیسترزیس شکل بالا رسم شده، حاصل از پوشِ منحنی‌ ها در هر سیکل بارگذاری می‌باشد (پوش یا Envelope در اینجا با وصل نمودن نقاط حداکثر نمودارها بدست می‌آید). در ادامه و در شکل زیر دو نمونه Backbone Curve برای دو حالت بارگذاری یکنواخت و سیکلی مشاهده می‌شوند.

ازآنجایی‌که در بارگذاری یکنواخت اثر خستگی مصالح دیده نمی‌شود، منحنی Backbone در حالت بارگذاری یکنواخت نسبت به حالت بارگذاری سیکلی متفاوت است. بدین معنا که اثر بارهای رفت و برگشتی سبب شده که مصالح تحت بارهای کوچک‌تری تسلیم شوند، در نتیجه منحنی مربوط به بارگذاری سیکلی کوچک‌تر از حالت بارگذاری یکنواخت می‌باشد.

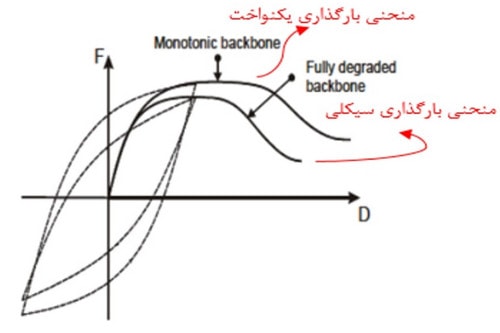
شکل 9: نمونه‌ای از منحنی‌های هیسترزیس و مقایسه‌ی backbone curve در دو حالت بارگذاری یکنواخت و سیکلی

نکته :

در بارگذاری سیکلی که در اولین شکل این بخش مشاهده می‌شود، در ابتدا مقاومت به دلیل رفتار سخت‌شوندگی افزایش یافته اما در نهایت، سختی (شیب منحنی) و مقاومت در اثر رفتار نرم‌شوندگی دچار کاهش شده‌اند و به اصطلاح، منحنی‌ها نسبت به حالت اولیه اندکی خوابیده‌تر شده‌اند. تفاوت منحنی‌های backbone در بارگذاری یکنواخت و سیکلی هم ناشی از همین مورد یعنی زوال سختی و مقاومت می‌باشد (Strength and Stiffness Degradation ).

اولین بار باشینگر (Bauschinger) متوجه رفتار متفاوت مواد، تحت بار رفت و برگشتی شد. او مشاهده کرد که اگر بارگذاری بر روی یک ماده در یک جهت (کشش یا فشار) تا رسیدن به تغییرشکل‌های پلاستیک ادامه یابد و سپس تغییر جهت داده شود، تنش تسلیم در جهت دیگر کاهش می‌یابد. به‌عنوان‌مثال در یک ماده با رفتار یکنواخت در کشش و فشار، انتظار داریم که تسلیم هم در کشش و هم در فشار تحت تنش   رخ دهد، اما درصورتی‌که این ماده تحت بار رفت و برگشتی ابتدا تحت کشش قرار گیرد مطابق انتظار، با رسیدن به تنش تسلیم  تسلیم شده و وارد ناحیه‌ی پلاستیک می‌شود، اما با تغییر جهت بارگذاری و اعمال بار فشاری، رفتار ماده مطابق انتظار نبوده و المان در تنشی کوچک‌تر از   تسلیم خواهد شد. این حالت درصورتی‌که ابتدا نمونه تحت‌فشار و سپس تحت کشش قرار گیرد هم صادق است.

در دو شکل زیر رفتار چرخه‌ای یک المان تحت بارگذاری متناوب مشاهده می‌شود. در شکل اول بارگذاری تا قبل از رسیدن به مرحله‌ی سخت‌شدگی کرنشی یا strain hardening متوقف شده و در واقع در ناحیه‌ی Yielding (که در بخش اول معرفی گردید) باقی می‌ماند. در این حالت اثر بوشینگر به خوبی قابل‌مشاهده است به‌طوری‌که پس از اعمال نیروی فشاری، در مرحله‌ی 6 به جای اینکه تا تنش σ_y– المان در حالت الاستیک باقی بماند، در تنشی کوچک‌تر از σ_y–  تسلیم شده است.

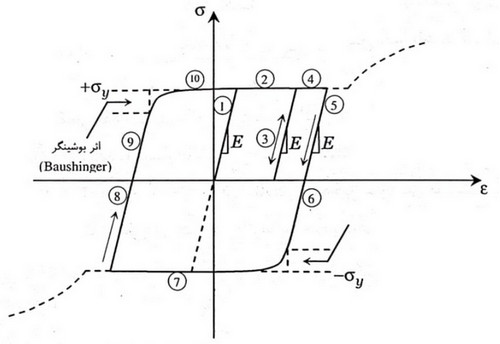
شکل 10: منحنی هیسترزیس برای حالتی که نمونه وارد سخت شدگی کرنشی نشده است

گام های بارگذاری منحنی هیسترزیس

در این شکل گام‌ های بارگذاری به صورت زیر می‌باشند:

1. بارگذاری تا رسیدن به تنش تسلیم
2. ادامه‌ ی بارگذاری در ناحیه‌ی تسلیم (Yielding).
3. بار برداری و بازگشت بخشی از جابه‌ جایی الاستیک المان، سپس بارگذاری دوباره به صورت کششی تا رسیدن به تنش تسلیم.
4. ادامه‌ ی بارگذاری تا قبل از رسیدن به ناحیه‌ی سخت‌ شوندگی کرنشی.
5. بار برداری و برگشت بخشی از جابه‌ جایی الاستیک المان.
6. ادامه‌ی روند بارگذاری این بار به صورت فشاری و تسلیم شدن در تنشی کوچک‌ تر از σ_y-.
7. ادامه‌ ی بارگذاری فشاری و افزایش کرنش در ناحیه‌ی تسلیم (Yielding) و توقف آن قبل از رسیدن به سخت‌ شوندگی کرنشی.
8. بار برداری تا رسیدن به تنش صفر و کاهش اندکی از کرنش که به صورت الاستیک بوده است.
9. بارگذاری به صورت کششی و تسلیم در تنشی کوچک‌ تر از σ_y .
10. بارگذاری کششی در ناحیه‌ی تسلیم تا قبل از رسیدن به ناحیه‌ ی سخت‌ شوندگی کرنشی.

در ادامه یک نمونه از بارگذاری متناوب دیگر در شکل زیر مشاهده می‌شود، با این تفاوت که این‌ بار در ناحیه‌ی سخت‌ شوندگی کرنشی (Strain Hardening) هم بارگذاری ادامه یافته است و سبب گشته در این حالت، سطح زیر منحنی نسبت به حالت قبل افزایش یابد.

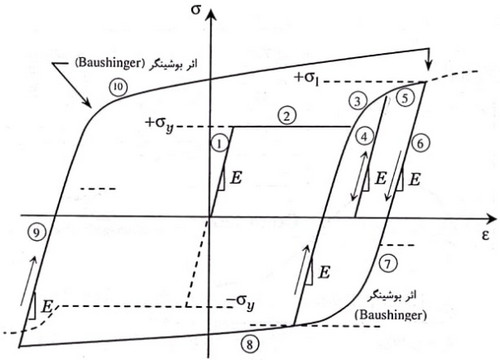
شکل 11: منحنی هیسترزیس برای حالتی که نمونه وارد سخت شدگی کرنشی شده است

4. ویژگی‌ منحنی هیسترزیس بررسی مفهوم جذب انرژی

در هنگام وقوع زلزله با توجه به ماهیت این بار، بارگذاری سازه به صورت سیکلی (رفت و برگشتی) خواهد بود. از این‌ رو، استفاده از نتایج آزمایش‌ هایی که در آن بارگذاری به صورت یکنواخت (Monotonic) انجام می‌شود، برای بررسی رفتار غیر‌خطی سازه و المان‌ های موجود در آن، قابل‌ قبول نیست، زیرا پارامتر های مهمی نظیر کاهندگی سختی و زوال مقاومت در ظرفیت شکل‌ پذیری، لحاظ نمی‌شوند.

سه ویژگی اصلی منحنی‌ های هیسترزیس که باعث می‌شود رفتار سازه و یا اعضای آن، تحت بار سیکلی مشخص شوند عبارت‌اند از:

• تقارن منحنی:هرچه تقارن منحنی تحت بارهای کششی و فشاری بیشتر باشد، نشان‌ دهنده‌ی یکنواختی رفتار عضو تحت بارگذاری‌های متناوب می‌باشد.
• سطح زیر نمودار منحنی:سطح زیر نمودار یا به عبارتی سطح محصور شده‌ی بین نمودارهای هیسترزیس نشان‌ دهنده‌ی انرژی مستهلک شده توسط عضو است. هرچه این سطح بزرگ‌تر باشد نشان‌ دهنده‌ی این است که عضو شکل‌ پذیرتر بوده و قابلیت جذب انرژی بیشتری دارد. در شکل زیر، انرژی جذب شده توسط المان مشاهده می‌شود.

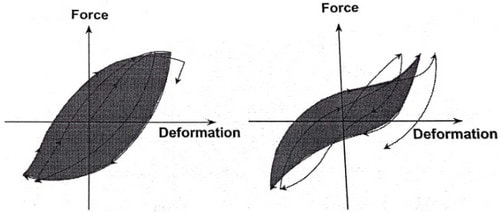
شکل 12: انرژی تلف شده در یک سیکل بارگذاری

• تعداد سیکل‌ها:تعداد سیکل‌ هایی هم که یک المان می‌توان تا قبل از گسیختگی تحمل نماید نشان‌ دهنده‌ی قابلیت اطمینان و پایداری عضو می‌باشد.

در شکل زیر یک منحنی هیسترزیس ایده‌ آل مشاهده می‌شود. در این نمودار، المان در طول بارگذاری دچار کاهش سختی و همچنین زوال مقاومت نشده و سطح زیر نمودار ثابت باقی مانده است.

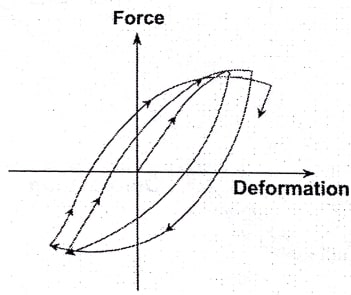
شکل 13:  نمونه‌ای از منحنی هیسترزیس بدون کاهش سختی و زوال مقاومت

در ادامه و در شکل زیر نمونه‌ای دیگر از منحنی هیسترزیس مشاهده می‌شود که سختی و مقاومت سازه (یا المان) تقریباً ثابت مانده اما به دلیل اینکه اثرات باریک‌شدگی (Pinching) در آن وجود دارد، قابلیت جذب انرژی هم کاهش‌ یافته است. پدیده‌ی باریک‌ شدگی منحنی در سازه‌ ها، گاهی اوقات به دلیل ضعف اتصالات و نرم شدن آن‌ ها اتفاق می‌افتد.

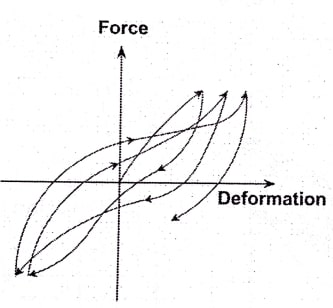
شکل 14: نمونه‌ای از منحنی هیسترزیس با اثر باریک شدگی (Pinching)

در شکل زیر هم  منحنی دچار زوال مقاومت و باریک‌ شدگی شده است و سطح زیر نمودار در مقایسه با نمودار ایده‌آل اولیه، بسیار کمتر شده است.

شکل 15: نمونه‌ای منحنی هیسترزیس که در آن پدیده‌ی باریک شدگی به همراه زوال مقاومت رخ داده است

5. انواع رفتار هیسترزیس مصالح

انواع رفتار هیسترزیس مصالح به چند بخش دسته بندی می‌شوند که عبارت‌اند از:

1.5. رفتار EPP: Elastoplastic Perfectly Plastic

یک رفتار ایده­آل هست که هیچ نوع زوال سختی و مقاومت در مصالح وجود ندارد وهمچنین در این حالت بیشترین اتلاف انرژی ایجاد می‌شود.

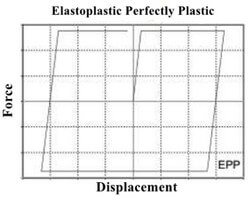
شکل 16: منحنی هیسترزیس مصالح با رفتار EPP

2.5. رفتار SD: Stiffness Degrading

در این حالت مقاومت مصالح بدون تغییر بوده و در طی سیکل­ های مختلف شاهد عدم کاهش مقاومت هستیم ولی در هر سیکل بارگذاری، مصالح دچار زوال سختی شده و در نتیجه آن منحنی هیسترزیس دچار جمع­شدگی (Pinching) می شود.

شکل 17: منحنی هیستزیس مصالح با رفتار SD

3.5. رفتار SSD: Stength and Stiffness Degrading

در این حالت، شاهد زوال سختی و مقاومت مصالح هستیم. به علت زوال سختی، منحنی هیسترزیس جمع شده و پدیده جمع­شدگی رخ می­دهد. بنابراین با زوال سختی و مقاومت در سیکل های متعدد، سطح زیر منحنی هیسترزیس کاهش یافته و توان اتلاف انرژی عضو پایین می­آید. در اکثر مصالح سازه­ای شاهد چنین رفتاری هستیم. به همین دلیل در روش ­های مختلف بهسازی و مقاوم­سازی در تلاش برای افزایش توان اتلاف انرژی هستند.

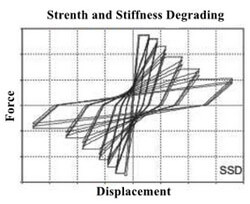
شکل 18: منحنی هیسترزیس مصالح با رفتار SSD

6. نمونه هایی از منحنی هیسترزیس اعضای سازه­ای

در ادامه برای درک بهتر نحوه‌ی تفسیر منحنی‌های هیسترزیس دو مثال‌ از این منحنی‌ها بررسی شده است. مثال‌های ذکر شده مربوط به اتصالات تیر به ستونی است که تحت بارهای سیکلی مورد بررسی قرار گرفته‌اند.

به طور مثال، در شکل زیر نمودار A3 و A4 مربوط به دو اتصال تیر به ستون هستند که اولی بدون سخت‌کننده‌ی قطری جان ستون ساخته شده، ولی نمونه‌ی A4 چشمه‌ی اتصال به کمک سخت‌کننده‌ی عرضی تقویت شده است. مشاهده می‌شود که در مدل A4 به دلیل وجود سخت کننده قطری مقاومت اتصال افزایش یافته ولی سطح زیر منحنی و در نتیجه جذب انرژی آن کاهش‌یافته است. به عبارتی می‌توان گفت در این حالت اتصال تردتر شده است.

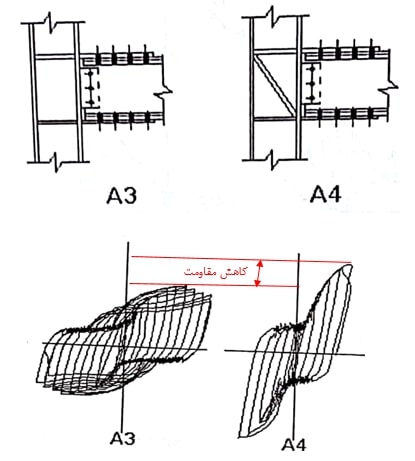
شکل 19: منحنی هیسترزیس دو اتصال تیر به ستون و بررسی اثر سخت‌کننده‌ی عرضی در جان ستون

منحنی‌های بعدی مربوط به دو اتصال می‌باشند که اتصالات آن به ستون توسط پیچ انجام شده و هر دو دارای قطعات لچکی متصل به ستون هستند. علاوه بر این‌ها در اتصال B4 سخت‌کننده‌هایی زیر بال ستون تعبیه شده است (برای کنترل تغییرشکل ایجاد شده توسط نیروی کششی پیچ‌های مقطع نبشی). مشاهده می‌شود که مقاومت در مقطع B4 که دارای سخت‌کننده است افزایش قابل ملاحظه‌ای داشته، همچنین سطح زیر نمودار هم بزرگ‌تر شده و نشان می‌دهد که جذب انرژی نمودار هم بهتر شده است.

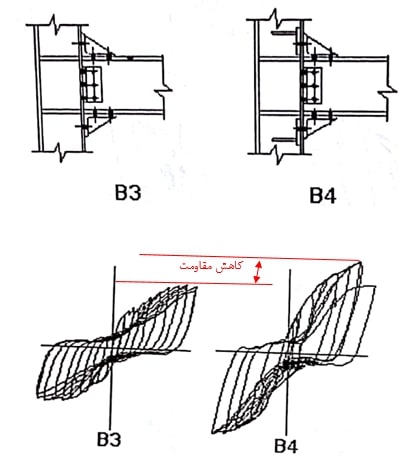
شکل 20:  منحنی هیسترزیس دو اتصال تیر به ستون و بررسی اثر سخت‌کننده‌ی زیر بال ستون

7. نتیجه گیری

همان­طور که می­دانیم زلزله یک تحریک شتاب­ دار است که انرژی بسیار زیادی را وارد سازه کرده و نیروهای عظیمی به سازه وارد می­کند. این انرژی بایستی به نحو مناسبی توسط اعضای سازه­ ای و از طریق رفتار غیرارتجاعی، مستهلک شود بدون آن­که پایداری عضو و سازه حفظ شود.

بنابراین برای مدل­سازی بهتر و دقیق ­تر سازه تحت بارهای لرزه­ ای نیازمند شناخت و فهم دقیق اعضای سازه ­ای هستیم. با توجه به این­که زلزله ماهیت رفت و برگشتی داشته و اعضای سازه­ ای به­ صورت سیکلیک بارگذاری می­شوند، شناخت منحنی­ های هیسترزیس از اهمیت بالایی برخوردار هستند، زیرا این منحنی­ ها میزان ظرفیت اعضا برای استهلاک انرژی زلزله را نشان داده و رفتار دقیق ­تر آن­ها را در طول ارتعاش نشان می­دهند.

میزان اتلاف انرژی که همان مساحت داخل منحنی­ های هیسترزیس است، به نوع مصالح و جزئیات اجرایی آن وابسته است.

منابع

1. کتاب تحلیل غیرخطی سازه، دکتر محمدرضا تابش پور، انتشارات فدک ایساتیس.
2. کتاب مقاومت مصالح (ایگور پوپوف)، ترجه ی مهندس شاپور طاحونی، انتشارات پارس آیین.
3. Material nonlinearity – Technical Knowledge Base, CSI America
4. Graham H.Powell, Modeling for Structural Analysis; Behavior and Basics. Computers and Structures Inc, University of Berkeley, USA, 2010

• مطلبی میخواهید که نیست ؟ از ما بپرسید تا برایتان محتوا رایگان تولید کنیم!

• ارسال سوال برای تولید محتوا